本篇教程中,我们会巩固上一篇所提到的矩阵和相机知识,并使用tdogl::Camera类来实现第一人称射击类型的相机。然后,我们会将相机与键盘和鼠标挂钩,使得我们可以移动和浏览3D场景。这里会学一些向量数学,还有上一篇没提到的逆矩阵。
获取代码
所有例子代码的zip打包可以从这里获取:https://github.com/tomdalling/opengl-series/archive/master.zip。
这一系列文章中所使用的代码都存放在:https://github.com/tomdalling/opengl-series。你可以在页面中下载zip,加入你会git的话,也可以复制该仓库。
本文代码你可以在source/04_camera目录里找到。使用OS X系统的,可以打开根目录里的opengl-series.xcodeproj,选择本文工程。使用Windows系统的,可以在Visual Studio 2013里打开opengl-series.sln,选择相应工程。
工程里已包含所有依赖,所以你不需要再安装或者配置额外的东西。如果有任何编译或运行上的问题,请联系我。
向量理论
在上一篇学了矩阵理论后,你以为数学理论课就结束了?想得太美了,现在下一部分就来了:向量。正统的理解认为向量是3D编程的基础。后面我会展示些代码,是用键盘来进行向量运算,让相机可以在不同方向上移动。
在3D中(2D中也一样),向量经常用来表示一些不同的东西,比如:
- 位置(即,坐标)
- 位移(比如,移动)
- 方向(比如,南北,上下)
- 速度(比如,车的速度和方向)
- 加速(比如,重力)
你可能注意到了上面所提的一些概念都是通常是用来实现物理引擎的。我们在本文中不会实现所有的物理,但为了更好的理解向量,第一步让我们来一些物理教学。
什么是向量?一种伪数学的定义上来说,一个向量(vector)就是幅度(magnitude)加上方向。它能向上,向下,往左,往右,朝北,朝西南等等。你能用3D向量来表示任何一个你指向的方向。向量的另一部分,幅度,表示向量的长度或者大小。
向量最简单的可视化方式就是绘制它,一般向量都会被绘制为箭头。箭头所指的方向就是向量的方向,箭头的长度就是幅度。下面的图是一个2D向量,但2D的理论同样能应用到3D上。
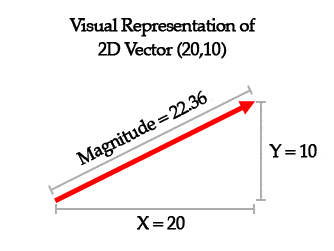
下面用例子来说明向量代表的不同含义。
| 方向 | 幅度 | 含义 | |
|---|---|---|---|
| 往北5千米 | 北 | 5千米 | 位置 |
| 头上5厘米 | 上 | 5厘米 | 位置 |
| 以50千米每小时开往西湖 | 西湖方向 | 50千米/每小时 | 速度 |
| 地球引力为9.8m/s2 | 往地球质心 | 9.8m/s2 | 加速 |
当编码时,向量只是一组数字。每个数字都是向量的“一维”。比如,一个三维3D向量就是有3个数字的数组,2D向量是有2个数字。因为我们是在3D中进行工作,所以大部分情况只要处理3D向量,但我们也需要用到4D。无论何时我说“向量”,那意味着是3D向量。我们使用GLM的向量数学库,2D,3D,4D的类型分别为glm::vec2
,glm::vec3,glm::vec4。
3D向量表示顶点,坐标或者位置相当简单。3D向量的3个维度分别是X,Y,Z的值。当向量表示位置,方向和幅度时,都是从原点(0,0,0)开始计算的。比如,假设一个物体的XYZ坐标为(0,2,0),则它的幅度是2,方向为“沿Y轴向上”。
负向量
当你要将向量取负时,就是保持相同的幅度,但变成了反方向。
比如:
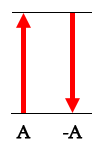
A=向北5千米
-A=向南5千米
如果相机的方向是往右的,我们可以使用负向量来算出相机往左的方向。就像这样:
glm::vec3 rightDirection = gCamera.right();
glm::vec3 leftDirection = -rightDirection; //vector negation
标量乘法
当你将向量乘上一个数值时,新向量的结果表示相同的方向,但幅度被扩大了相应倍数。这个数值被称为“标量”,这就是为何该乘法被称为“标量乘法”。
比如:
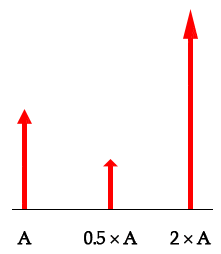
A=向北5千米
0.5 × A=向北2.5千米
2 × A=向北10千米
我们可以使用标量乘法来计算基于“移动速度”的相机位置,像这样:
const float moveSpeed = 2.0; //units per second
float distanceMoved = moveSpeed * secondsElapsed;
glm::vec3 forwardDirection = gCamera.forward();
glm::vec3 displacement = distanceMoved * forwardDirection; //scalar multiplication
向量加法
向量加法在2D图形表现下最容易理解。对两个向量进行加法,就是将它们的头部(箭头一段)连接尾部(非箭头一段)。加法顺序不重要。它的结果就是,从第一个向量尾部走向另外一个向量的头部。
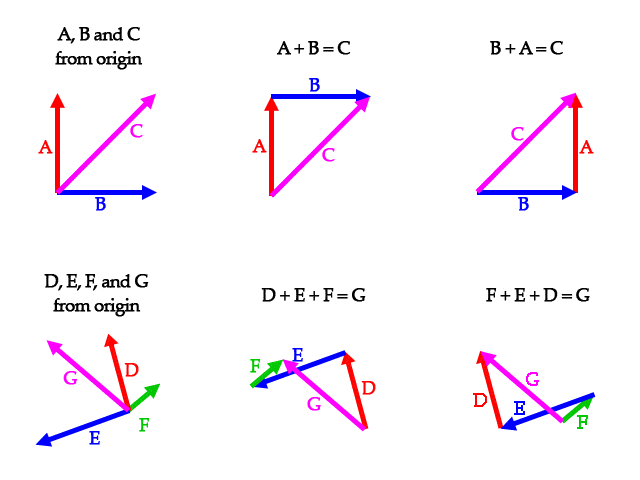
注意,即使这些向量看上去是在不同的位置上,但结果向量的幅度(长度)和方向不会改变。请记住,向量只有一个方向和一个幅度。它们没有起始点,所以它们可以在任意不同位置上,但还是相等的。
比如:
A = 往北1千米
B = 往西1千米
A + B = 往西北1.41千米
向量减法相当于是加上一个负向量,比如:
A = 往北1千米
B = 往西1千米
A - B = 往西北1.41千米
A + (-B) = 往西北1.41千米
我们使用向量加法来计算出相机位移后的的新位置,像这样:
glm::vec3 displacement = gCamera.forward() * moveSpeed * secondsElapsed;
glm::vec3 oldPosition = gCamera.position();
glm::vec3 newPosition = oldPosition + displacement; //vector addition
gCamera.setPosition(newPosition);
单位向量
单位向量是幅度为1的向量。它们经常被用来表示方向。
当一个向量是用来表示方向时,它的幅度就没啥用处。即使这样,我们还是将它的幅度设为1,是为了计算时更方便一些。
当你在单位向量上使用标量乘法时,它的方向仍然不变,但幅度会被设为标量的值。因此,你将一个单位向量乘上5后,新的向量的幅度就是5。假如你乘上123,那幅度也就是123。基本上这允许我们设置任意一个向量的幅度,而不会更改它的方向。
让我们对相机进行往左移动12单位的操作。我们先设置一个方向为左的单位向量,然后使用标量乘法将它的幅度设为12,最后使用它来计算出新位置。代码看上去应该是这样的:
// `gCamera.right()` returns a unit vector, therefore `leftDirection` will also be a unit vector.
// Negation only affects the direction, not the magnitude.
glm::vec3 leftDirection = -gCamera.right();
//`displacement` will have a magnitude of 12
glm::vec3 displacement = leftDirection * 12;
//`newPosition` will be 12 units to the left of `oldPosition`
glm::vec3 newPosition = oldPosition + displacement;
任何一个向量都能变为单位向量。这个操作叫做单位化。我们可以用GLM来单位化一个向量:
glm::vec3 someRandomVector = glm::vec3(123,456,789);
glm::vec3 unitVector = glm::normalize(someRandomVector);
tdogl::Camera类
恭喜你看到这儿了!现在你已经有足够的向量知识了,来,让我们开始编码。
tdogl::Camera类的接口在这里,实现代码在这里。
在前面文章中我们在OpenGL中用矩阵来实现相机。tdogl::Camera类可以基于各种属性来创建矩阵,比如:
- 相机位置
- 相机朝向(方向)
- 缩放(视野)
- 最大和最小可视距离(远近平面)
- 视口/窗口纵横比
上面的每个属性都有各自的设置和获取接口。前文已经介绍过了。
现在让我们用matrix和orientation方法来实现如何让这所有属性组合成一个矩阵。
glm::mat4 Camera::matrix() const {
glm::mat4 camera = glm::perspective(_fieldOfView, _viewportAspectRatio, _nearPlane, _farPlane);
camera *= orientation();
camera = glm::translate(camera, -_position);
return camera;
}
glm::mat4 Camera::orientation() const {
glm::mat4 orientation;
orientation = glm::rotate(orientation, _verticalAngle, glm::vec3(1,0,0));
orientation = glm::rotate(orientation, _horizontalAngle, glm::vec3(0,1,0));
return orientation;
}
我们可以看到,最终的相机矩阵是由四个不同的变换组成。按顺序是:
- 移动,基于相机位置
- 旋转,基于相机水平(左/右)转角
- 旋转,基于相机垂直(上/下)转角
- 透视,基于视野,近平面,远平面和纵横比
假如你觉得这顺序是反的,那请记住矩阵乘法是从右往左,代码上顺序是从底往上。
注意,移动用了相机的负位置。这里再次用前文提到的方式,我们可以让3D场景往后来实现相机往前走。向量为负时会反转其方向,所以“往前”就变成“往后”。
tdogl::Camera类还有其它方法来返回单位向量:上,右和前。我们需要从键盘获取消息来实现相机移动。
相机方位矩阵求逆
让我来看下tdogl::Camera::up方法的实现,这里有两个东西我们还没有提及。
glm::vec3 Camera::up() const {
glm::vec4 up = glm::inverse(orientation()) * glm::vec4(0,1,0,1);
return glm::vec3(up);
}
我们看到它使用了glm::inverse方法。从上一篇文章中,我们知道矩阵能对坐标进行变换。在这里,我们还需要对坐标进行“反变换”,使得我们能获得矩阵乘法变换前的坐标。为了实现这个目的,我们需要计算逆矩阵。逆矩阵是一个矩阵,完全相反于另外一个矩阵,这意味着它能撤销另外一个矩阵的变换。比如,矩阵A是绕着Y轴旋转90°,那矩阵A的逆矩阵就是绕着Y轴旋转-90°。
当相机的方向改变时,“向上”的方向也随之改变。比如,想象下有个箭头指向你的头顶,假如你旋转你的头往地上看,那箭头就是向前倾斜,假如你往天上看,那箭头是向后倾斜的。如果你往前看,就是你的头“不旋转”,那箭头就是笔直向上。我们用“笔直向上”的单位向量(0,1,0)来表示相机的向上方向,“不旋转”使用相机方位矩阵的逆矩阵。另外一种解释,在相机旋转后,向上方向总是为(0,1,0),所以我们要将逆旋转乘上(0,1,0),这就能得到相机旋转前的向上方向。
(0,1,0)是单位向量,当你旋转一个单位向量结果还是一个单位向量。假如结果不是单位向量,你应该使用glm::normalize来单位化。
计算相机的前和右方向是同样的方式。
你可能注意到了这里用了一个4D向量glm::vec4。前文解释过,4x4 矩阵(glm::mat4)需要一个4D向量来进行矩阵乘法,使用glm::vec3会导致编译错误。只要把3D向量(0,1,0)变成4D向量(0,1,0,1)就可以进行矩阵乘法了,计算完成后我们再将4D向量变回3D向量。
整合tdogl::Camera类
现在我们开始使用tdogl:Camera类。
在之前的文章中,我们分别设置了投影矩阵和相机矩阵两个着色器变量。在本文中,tdogl::Camera合并了这两个矩阵,所以让我们移除projection着色器变量,只用camera变量就足够了。下面是顶点着色器的更新:
#version 150
uniform mat4 camera;
uniform mat4 model;
in vec3 vert;
in vec2 vertTexCoord;
out vec2 fragTexCoord;
void main() {
// Pass the tex coord straight through to the fragment shader
fragTexCoord = vertTexCoord;
// Apply all matrix transformations to vert
gl_Position = camera * model * vec4(vert, 1);
}
现在我们将tdogl::Camera整合到main.cpp中。首先包含头文件:
#include "tdogl/Camera.h"
然后声明全局变量:
tdogl::Camera gCamera;
在前一篇文章中,相机和投影矩阵是不会改变的,所以在LoadShaders函数中设置一次就好了。但在本文中,因为我们需要用鼠标和键盘来控制,所以设置相机矩阵要放在Render函数中并每帧都要设置一下。首先让我们移除旧代码:
static void LoadShaders() {
std::vector<tdogl::Shader> shaders;
shaders.push_back(tdogl::Shader::shaderFromFile(ResourcePath("vertex-shader.txt"), GL_VERTEX_SHADER));
shaders.push_back(tdogl::Shader::shaderFromFile(ResourcePath("fragment-shader.txt"), GL_FRAGMENT_SHADER));
gProgram = new tdogl::Program(shaders);
// the commented-out code below was removed
/*
gProgram->use();
//set the "projection" uniform in the vertex shader, because it's not going to change
glm::mat4 projection = glm::perspective<float>(50.0, SCREEN_SIZE.x/SCREEN_SIZE.y, 0.1, 10.0);
//glm::mat4 projection = glm::ortho<float>(-2, 2, -2, 2, 0.1, 10);
gProgram->setUniform("projection", projection);
//set the "camera" uniform in the vertex shader, because it's also not going to change
glm::mat4 camera = glm::lookAt(glm::vec3(3,3,3), glm::vec3(0,0,0), glm::vec3(0,1,0));
gProgram->setUniform("camera", camera);
gProgram->stopUsing();
*/
}
然后,在Render函数中设置camera着色器变量:
// draws a single frame
static void Render() {
// clear everything
glClearColor(0, 0, 0, 1); // black
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
// bind the program (the shaders)
gProgram->use();
// set the "camera" uniform
gProgram->setUniform("camera", gCamera.matrix());
gCamera.matrix()函数返回的是一个glm::mat4, 并且setUniform函数使用了glUniformMatrix4fv来设置顶点着色器中的相机矩阵uniform变量。
在AppMain函数中设置相机的初始化位置和视窗纵横比。
gCamera.setPosition(glm::vec3(0,0,4));
gCamera.setViewportAspectRatio(SCREEN_SIZE.x / SCREEN_SIZE.y);
其余相机属性都留成默认值。
你现在运行程序,会看到上次实现的旋转立方体。下一步就让我们用鼠标和键盘来控制相机。
键盘输入
我们先来实现键盘控制。每次我们更新屏幕时,我们先检查’W',‘A’,‘S’或’D’按键是否被按下,如果有触发那就稍微移动下相机。函数glfwGetKey返回一个布尔值来表示这个按键是否按下。新的Update函数看上去是这样的:
// update the scene based on the time elapsed since last update
void Update(float secondsElapsed) {
//rotate the cube
const GLfloat degreesPerSecond = 180.0f;
gDegreesRotated += secondsElapsed * degreesPerSecond;
while(gDegreesRotated > 360.0f) gDegreesRotated -= 360.0f;
//move position of camera based on WASD keys
const float moveSpeed = 2.0; //units per second
if(glfwGetKey(gWindow, 'S')){
gCamera.offsetPosition(secondsElapsed * moveSpeed * -gCamera.forward());
} else if(glfwGetKey(gWindow, 'W')){
gCamera.offsetPosition(secondsElapsed * moveSpeed * gCamera.forward());
}
if(glfwGetKey(gWindow, 'A')){
gCamera.offsetPosition(secondsElapsed * moveSpeed * -gCamera.right());
} else if(glfwGetKey(gWindow, 'D')){
gCamera.offsetPosition(secondsElapsed * moveSpeed * gCamera.right());
}
}
我们先忽略立方体的旋转。
当S键被按下时,我们可以看得更近些:
gCamera.offsetPosition(secondsElapsed * moveSpeed * -gCamera.forward());
这一行代码做了好多事,让我们用更容易懂的方式重写一遍,新的函数叫MoveCameraBackwards。
void MoveCameraBackwards(float secondsElapsed) {
//TODO: finish writing this function
}
向后是一个方向,所以应该是个单位向量。在相机类中没有backward函数,但它有个forward函数。向后就是向前的反方向,所以我们只要对向前的单位向量取负数即可。
void MoveCameraBackwards(float secondsElapsed) {
//`direction` is a unit vector, set to the "backwards" direction
glm::vec3 direction = -gCamera.forward();
//TODO: finish writing this function
}
然后,我们应该知道将相机移多远。我们有相机的移动速度moveSpeed,我们还知道从上一帧到现在过去了多少时间secondsElapsed。对这两个值进行乘法,就能得到相机移动的距离。
void MoveCameraBackwards(float secondsElapsed) {
//`direction` is a unit vector, set to the "backwards" direction
glm::vec3 direction = -gCamera.forwards();
//`distance` is the total distance to move the camera
float distance = moveSpeed * secondsElapsed;
//TODO: finish writing this function
}
现在,我们知道了移动的距离和方向,我们就能构造一个位移向量。它的幅度就是distance,它的方向就是direction。因为direction是个单位向量,我们可以用标量乘法来设置幅度。
void MoveCameraBackwards(float secondsElapsed) {
//`direction` is a unit vector, set to the "backwards" direction
glm::vec3 direction = -gCamera.forwards(); //vector negation
//`distance` is the total distance to move the camera
float distance = moveSpeed * secondsElapsed;
//`displacement` is a combination of `distance` and `direction`
glm::vec3 displacement = distance * direction; //scalar multiplication
//TODO: finish writing this function
}
最后,我们移动(或者说是置换)相机当前位置。用向量加法即可。最基础的公式newPosition = oldPosition + displacement。
void MoveCameraBackwards(float secondsElapsed) {
//`direction` is a unit vector, set to the "backwards" direction
glm::vec3 direction = -gCamera.forwards(); //vector negation
//`distance` is the total distance to move the camera
float distance = moveSpeed * secondsElapsed;
//`displacement` is a combination of `distance` and `direction`
glm::vec3 displacement = distance * direction; //scalar multiplication
//change the position of the camera
glm::vec3 oldPosition = gCamera.position();
glm::vec3 newPosition = oldPosition + displacement; //vector addition
gCamera.setPosition(newPosition);
}
完成了!MoveCameraBackwards函数这么多行代码跟这一行代码是一样的:
gCamera.offsetPosition(secondsElapsed * moveSpeed * -gCamera.forward());
offsetPosition函数做的就是向量加法,它将位移向量作为参数传入。让我们使用那一行代码来替换MoveCameraBackwards函数,因为简洁就是美。
其余按键的工作方式都是相同的,无非是方向不同而已。让我们再添加Z和X键来实现相机上和下。
if(glfwGetKey(gWindow, 'Z')){
gCamera.offsetPosition(secondsElapsed * moveSpeed * -glm::vec3(0,1,0));
} else if(glfwGetKey(gWindow, 'X')){
gCamera.offsetPosition(secondsElapsed * moveSpeed * glm::vec3(0,1,0));
}
注意,为什么这里用向量(0,1,0)而不是gCamera.up()。记住,“向上”方向会随着相机方向而改变。假如相机看地上,“向上”指的是向前,假设相机看天上,“向上”指的是向后。这并不是我想实现的行为,我希望的是“笔直向上”的方向(0,1,0),不依赖于相机的方向。
现在当你运行程序,你能使用W, A, S, D, X,和Z键来向前移动,向左移动,向后移动,向右移动,向上移动和向下移动。观察时不会因为相机移动而改变方向,这个将留个鼠标来控制。
鼠标输入
此时,我们的窗口还无法捕捉鼠标消息。你能看到鼠标在窗口上移来移去。我希望它消失,并且不希望它移出窗口。为了实现这个,我们要改下GLFW的设置。
在我们捕获鼠标之前,让我们先实现用取消键(Esc)退出程序。我不想再点击关闭按钮了,因为鼠标隐藏,并且无法离开窗口。让我们在AppMain主循环下放加上些代码:
// run while the window is open
double lastTime = glfwGetTime();
while(!glfwWindowShouldClose(gWindow)){
// process pending events
glfwPollEvents();
// update the scene based on the time elapsed since last update
double thisTime = glfwGetTime();
Update((float)(thisTime - lastTime));
lastTime = thisTime;
// draw one frame
Render();
// check for errors
GLenum error = glGetError();
if(error != GL_NO_ERROR)
std::cerr << "OpenGL Error " << error << std::endl;
//exit program if escape key is pressed
if(glfwGetKey(gWindow, GLFW_KEY_ESCAPE))
glfwSetWindowShouldClose(gWindow, GL_TRUE);
}
当我们用glfwCreateWindow打开窗口这样设置时,就可以捕获鼠标了:
// GLFW settings
glfwSetInputMode(gWindow, GLFW_CURSOR, GLFW_CURSOR_DISABLED);
glfwSetCursorPos(gWindow, 0, 0);
这段代码让鼠标消失了,并且将它移动到了像素坐标(0,0)。在Update中,我们会获取鼠标位置来更新相机,更新完后将鼠标坐标再次设为(0,0)。这种方式可以很方便的看出每帧鼠标移动了多少,还要在当鼠标要移出窗口时停住它。在Update函数下面添加以下代码:
//rotate camera based on mouse movement
const float mouseSensitivity = 0.1f;
double mouseX, mouseY;
glfwGetCursorPos(gWindow, &mouseX, &mouseY);
gCamera.offsetOrientation(mouseSensitivity * (float)mouseY, mouseSensitivity * (float)mouseX);
glfwSetCursorPos(gWindow, 0, 0); //reset the mouse, so it doesn't go out of the window
鼠标的坐标单位是像素,但相机方向是基于两个角度。这就是为何我们使用mouseSensitivity变量来将像素转为角度。越大的鼠标灵敏度,相机转向的越快,越小的灵敏度,转向的越慢。灵敏度设为0.1f的含义就是每10像素就旋转1°。
offsetOrientation函数类似于offsetPosition函数,它会使用水平和垂直角度来更新相机方向。
好了!基本到这就完成了。你现在运行程序的话,你能绕着飞行并且几乎能观察任意方向。立方体的旋转动画可能会让你在环绕时失去方向感,我们可以关闭它。
用鼠标滚轮控制视野
就像蛋糕上的糖衣一样,我们可以滚动鼠标或者在触摸板上滑动来实现相机镜头的视野缩放。上篇文章我们已经解释过视野的概念了。
我们使用同样的方式来使用鼠标位置,并且每帧重置滚动值。首先我们创建一个全局变量来保存滚动值:
double gScrollY = 0.0;
使用GLFW来接受滚轮消息,首先我们得创建个回调:
// records how far the y axis has been scrolled
void OnScroll(GLFWwindow* window, double deltaX, double deltaY) {
gScrollY += deltaY;
}
然后我们用GLFW在AppMain中注册下回调:
glfwSetScrollCallback(gWindow, OnScroll);
当每帧我们渲染的时候,我们使用gScrollY值来更改视野。代码放在Update函数的下放:
const float zoomSensitivity = -0.2f;
float fieldOfView = gCamera.fieldOfView() + zoomSensitivity * (float)gScrollY;
if(fieldOfView < 5.0f) fieldOfView = 5.0f;
if(fieldOfView > 130.0f) fieldOfView = 130.0f;
gCamera.setFieldOfView(fieldOfView);
gScrollY = 0;
zoomSensitivity常量类似mouseSensitivity常量。视野取值范围是0°到180°,但假如你设置的值离上下限很近的话,3D场景看上去会很奇怪,所以我们限制这个值范围在5°到130°。类似鼠标位置的方法,我们在每帧之后设置gScrollY = 0。
下篇预告
下一篇文章,我们会重构代码来实现最最基本的“引擎”。我们会将代码分为资产(资源)和实例,类似典型的3D引擎,可以生成有多个略微不同的木箱子的3D场景。
更多资源
- The vector math chapter of Learning Modern 3D Graphics Programming by Jason L. McKesson
- Vector maths – a primer for games programmers
- Basic 3D Math: Vectors by Egon Rath
- Wikipedia article on vectors, which isn’t very beginner-friendly
- The GLFW guides and references.
- 假如你有任何关于向量方面对初学者友好的文章,请发送给我,我会添加进来。